4 Brillouin’s Beschreibung des zeitlichen Signalverhaltens mittels der Sattelpunktmethode
In der an Sommerfeld anschließenden Arbeit von 1914 mit demselben Titel führte Brillouin die Untersuchungen zum Zeitverhalten fort [1, 2]. Dabei benutzt er jedoch nicht den von Sommerfeld vorgeschlagenen Integrationsweg über die Polstellen und Verzweigungsschnitte mit den sich kompensierenden Integrationswegen nach Unendlich, sondern legt den Weg so, daß dieser außer an den zeitlich beweglichen Sattelpunkten vernachlässigbare Beiträge zum Integral liefert. In solche Gebiete gelangt man durch Fallinien, welche von den Sattelpunkten ausgehen.
Brillouin konnte für den normalen Dispersionsbereich zeigen, daß die Signalgeschwindigkeit mit der Gruppengeschwindigkeit übereinstimmt und auch einen Intensitätsschwellwert für den Detektor angeben, der die Ankunft des Signals definiert und den er auf ein viertel der ursprünglichen Intensität festlegt.
4.1 Grundlegende Begriffe, komplexzahlige Phasenebene und Symmetrien
Zur Beschreibung des Signals verwendet Brillouin analog zu Sommerfeld die Darstellung
wobei
und
ist. Für den Exponenten wird die Funktionen
mit
eingeführt. Dabei wurde die Dispersionsbeziehung
verwendet und der dimensionslose Parameter
eingeführt. Für
ist das Signal am Ort
an noch nicht existent. Es kommt dort erst mit Vakuumlichtgeschwindigkeit an, wenn
wird. Wie bereits oben definiert ist
die retardierte Zeit, hier ausgedrückt durch den dimensionslosen Parameter
Die analytische Funktion
läßt sich durch den Realteil
und den Imaginärteil
darstellen. Es sei
, dann bestätigt man zunächst mit
und
, daß
gleich dem konjugiert Komplexen von
ist, d. h.
. Folglich ist
und weiter
Damit gilt wegen
die Symmetrieeigenschaft
.
4.2 Die Methode der Sattelpunkte
Obwohl der Integrationsweg in (\ref{eq:Signaldarstellung_Brillouin}↓), solange keine Singularitäten und Verzweigungsschnitte übersprungen werden, zur Auswertung beliebig deformiert werden kann, ist es für die numerische Berechnung bzw. zur Bestimmung einer Näherungslösung zweckmäßig, den Weg so zu legen, daß möglichst nur über kleine Funktionswerte integriert werden muß, d. h.
sollte darauf möglichst große negative Werte annehmen. Die harmonische Funktion
besitzt lokal keine endlichen Maxima oder Minima, jedoch zwischen den Erhebungen Sattelpunkte, von denen man entlang der Fallinien in die Täler gelangt. Ist der Funktionsabstieg dort sehr steil (Methode des steilsten Abstiegs), dann liefert bereits die Integration auf einem kleinen Wegabschnitt über die Sattelpunkte die wesentlichen Beiträge zum Gesamtintegral (\ref{eq:Signaldarstellung_Brillouin}↓). Die Methode der Sattelpunkte wurde bereits 1909 von Peter Debye bei der Bestimmung von Näherungsformeln für Zylinderfunktion in [3] benutzt.
Ein Sattelpunkt
muß die notwendige Bedingung
bzw.
und
erfüllen. Angewendet auf (\ref{eq:Exponent_w_z}↓) besteht die Forderung
bzw.
Ist
, so gelangt man von den Sattelpunkten über die Fallinien in Gebiete mit großen negativen Werten für
, in denen dann der Anteil zum Integral vernachlässigbar ist. Ist das Gefälle ins Tal groß, so kann man den Integrationsweg durch ein tangentiales Geradenstück ersetzen. Mit dem Ansatz
, wobei
und
diese Gerade um den Sattelpunkt parametrisieren, versucht man
auf die quadratische Form
zu bringen, wobei der Koeffizient
reell und positiv ist. Die vom Sattelpunkt ausgehenden Fallinien bilden dann mit der reellen Achse den Winkel
Er wird wegen des geforderten Integrationswegs von
nach
so gewählt, daß
gilt. Das gesamte Integrationsweg setzt sich aus den über die Sattelpunkte
führenden Teilpfaden zusammen, so daß man das Gesamtintegral (\ref{eq:Signaldarstellung_Brillouin}↓) in Summe der Teilintegrale
zerlegen kann. Ist
groß genug, so daß ein merklicher Abfall der Exponentialfunktion auf einem sehr kurzen Wegabschnitt erfolgt und ändert sich
dabei kaum, so kann das Integral auch von
kommend nach
über
erstreckt werden, wobei
konstant
gehalten werden kann. Somit ist vereinfacht
und nach Auswertung des Integrals
Die Güte der Näherung hängt von der Größe des Parameters
ab.
Es kann vorkommen, daß
am Sattelpunkt verschwindet. Dann muß man für
– abgesehen vom konstanten Ausdruck
– eine Entwicklung in höheren Potenzen ansetzen, z. B. in
. Für die Fallinien gibt es dann mehr als zwei Richtungen, von denen zwei geeignete für den Integrationsweg gewählt werden.
4.3 Zeitabhängige Lage der Sattelpunkte für große und kleine komplexzahlige Argumente
Die Lage der für die Integration wesentlichen Sattelpunkte
ist wegen
vom Zeitparameter
abhängig. Für den komplexzahligen Brechungsindex
wird wieder des Lorentzsche Dispersionsmodell
verwendet.
Kurz nach der Ankunft des Signals ist
. Die Gleichung (\ref{eq:Theta_Bedingung_Sattelpunkte}↓) wird für betragsmäßig große
erfüllt, da dann
gilt. Außerdem verschwindet der hintere Term. Für sehr große Werte
nähern sich die Sattelpunkte den Punkten der beiden symmetrisch liegenden Verzweigungsschnitte. Einerseits wird dort
unendlich an den singulären Punkten
, anderseits
unendlich an den Nullstellen
.
Die Untersuchungen zum Signalverhalten werden erleichtert, wenn man für das komplexzahlige Frequenzverhalten des Brechungsindex vereinfachende Annahmen macht. Dann läßt sich die Lage der Sattelpunkt näherungsweise aus quadratischen Gleichungen bestimmen und damit die Phasenfunktion
berechnen.
Es soll zunächst das Verhalten der Phasenfunktion an den Sattelpunkten für betragsmäßig kleine Werte
, d. h.
und
mit
, unter der Bedingung sehr kleiner Dämpfung (
) bestimmt werden. Mit den Parametern
und
lautet
näherungsweise
Folglich berechnen sich die Sattelpunkte wegen (\ref{eq:Definition_Sattelpunkt}↓) aus der quadratischen Gleichung
welche die beiden Lösungen
besitzt. Die Lage der Sattelpunkte in der komplexen Ebene kann entsprechend des Vorzeichens von
klassifiziert werden. Für
liegen die Sattelpunkte symmetrisch auf der Geraden
bei
Die Fallinien bilden für
einen Winkel
und für
einen Winkel
mit der reellen Achse.
Für große Werte
, d. h. für
und
, gilt näherungsweise
Die hieraus bestimmten Sattelpunkte liegen bei
also symmetrisch um den Punkt
auf der durch diesen Punkt gehenden Geraden
. Für kleine positive Zeiten
sind die Realteile der Sattelpunkte sehr groß und es gilt näherungsweise
. Mit fortschreitenden Zeiten
verringert sich betragsmäßig ihr Realteil, bis schließlich der Gültigkeitsbereich der Näherung verlassen wird. Die Fallinien in den Sattelpunkten bilden für
einen Winkel
und für
einen Winkel von
mit der reellen Achse.
Gemäß der Bedingung (\ref{eq:Theta_Bedingung_Sattelpunkte}↓) und der Beziehung (\ref{eq:Brechungsindex_Sattelpunkte}↓) kann man die Sattelpunkte allgemein aus der resultierenden algebraischen Gleichung 8. Grades
mit den zugehörigen zeitabhängigen Koeffizienten
berechnen, was mit numerischen Verfahren möglich ist. Nicht alle Lösungen sind Sattelpunkte im üblichen Sinne, sondern weisen in gewissen Richtungen wendekurvenartiges Verhalten auf. Dies betrifft speziell die vier ober- bzw. unterhalb des Verzweigungsschnittes im Absorptionsstreifen liegenden Lösungen. Sie werden bei den weiteren Untersuchungen jedoch nicht benötigt. Die vier verbleibenden Lösungen weisen je nach
Lagesymmetrien auf, so daß insgesamt nur zwei Sattelpunkte in der Auswertung berücksichtigt werden müssen.
4.4 Signal- und Gruppengeschwindigkeit
Mit der Integration entlang des Weges in der komplexen Ebene erfolgt eine gewichtete Überlagerung von Schwingungsanteilen mit Frequenzen, die zum Sattelpunkt benachbart liegen. Im Fall reeller Werte
bestimmt ein solcher Sattelpunkt die Gruppengeschwindigkeit
. Man kann annehmen, daß sich auch die Wellengruppe (Superposition der Wellen) in der Nähe dieses Sattelpunktes mit dieser Geschwindigkeit fortpflanzen. Ist die Anregungsfrequenz
weit von der Eigenfrequenz
des Mediums entfernt, so kann man die am Sattelpunkt berechnete Gruppengeschwindigkeit als Signalgeschwindigkeit definieren. Dies ist für Sattelpunkte
mit betragsmäßig kleinen
der Fall, die sich für größere Zeiten entlang der Geraden
bewegen. An einem solchen gibt es eine Fallinie steilsten Abstiegs, deren Projektion die reelle Achse im Punkt
schneidet. Brillouin definiert die Ankunft des Signals durch den Zeitpunkt
, in dem der Punkt
die Polstelle
erreicht und dort das Signal fast die volle Amplitude annimmt. In der Umgebung von Sattelpunktes
existiert ein Punkt mit gleichem Realteil, an dem die Projektion der Fallinie die reelle Achse im Punkt
berührt. Da die Abstände
und
gewöhnlich sehr klein sind, ließe sich die Ankunft des Signals auch näherungsweise durch das Aufeinandertreffen von
in
definieren. Mit
wird
Für die durch
verlaufende Niveaulinie gilt
und folglich
. Aus letzterer Bedingung erhält man
wodurch die Gruppengeschwindigkeit
definiert werden kann. Damit würde der Zeitpunkt
die Ankunft die Signals am Ort
beschreiben.
4.5 Einschwingverhalten, erster und zweiter Vorläufer
Es sollen zunächst die Sattelpunkte bei betragsmäßig kleinen Werten
betrachtet werden. Im Fall, daß
gilt, kann mit den in der Optik üblichen physikalischen Parametern (z. B.
,
bei
bzw.
,
,
und damit
sowie
) gezeigt werden, daß der Beitrag dieses Sattelpunktes zum Signal vernachlässigbar klein bleibt. Er nimmt erst mit dem Übergang
deutlich zu. Das zeitliche Übergangsverhalten in der Umgebung
soll später beschrieben werden
Der Fall
führt zu einem merklichen Einschwingverhalten, daß sich von der von Sommerfeld gefundenen Lösung unterscheidet und für größere Zeiten gültig ist. Dieser Abschnitt der Signalankündigung wird nach Brillouin gleichfalls Vorläufer genannt. In diesem Fall verläuft der Integrationsweg über die Sattelpunkte
mit
unter einem Winkel
. Man kann in deren Umgebung die quadratische Entwicklung
mit den Funktionswerten
finden, wobei
,
und
gilt. Entsprechend (\ref{eq: Sattelpunktsnaeherung}↓) wird für hinreichend große Werte
, etwa
, nach Bildung des Realteils
In der Regel kann man
gegenüber
vernachlässigen, so daß sich die Lösung zu
vereinfacht. Man beachte, daß
für
negativ ist und eine zeitliche Dämpfung der Amplitude bedeutet. Nähert sich
dem Wert 0, dann nimmt der Exponentialausdruck maximal den Wert 1 an. Gleichfalls wächst der Wurzelausdruck, da dann
kleiner wird. Jedoch verliert bei zu kleinem
die Sattelpunktnäherung wegen der Forderung an
und damit für
ihre Gültigkeit. Außerdem darf sich
nicht zu nahe dem singulären Punkt mit der Schwingungsdauer
des eintreffenden Signals nähern. Unter der Bedingung, daß
klein gegenüber
ist, beträgt die maximale Amplitude näherungsweise
So erhält man für obige Beispielparameter und
den Wert
. Wegen der Kleinheit von
und falls der Sattelpunkt weit weg von der Polstelle
liegt (
), überwiegt der erste Term im hinteren Klammerausdruck. Rückt der Sattelpunkt mit wachsender Zeit in die Nähe der Anregung, dann gewinnt der zweite Term an Gewicht, was mit einer deutlichen Änderung der Amplitude verbunden ist. Durch die Überlagerung mit dem ersten Term ergibt sich ein änderndes Phasenverhalten. Den in (\ref{eq:Brillouin_Vorlaeufer_2}↓) bestimmten Zeitabschnitt des eintreffenden Signals, der sich aus der Sattelpunktlösung für Argumente nahe dem Ursprung ergibt, bezeichnet Brillouin als zweiten Vorläufer. Dieser setzt in der Nähe von
ein, d. h. ungefähr zum Zeitpunkt
. Das zeitliche Verhalten ist wegen der Abhängigkeit der Phasenfunktion von
materialabhängig.
Für die zeitliche Änderung der Phase
am Ort
folgt
Wegen
ist
, so daß näherungsweise
gilt. Die zeitliche Phasenänderung
stimmt mit dem Realteil des Sattelpunktes überein, der sich mit der Gruppengeschwindigkeit
bewegt (s. o.).
Bei der Herleitung wurden in Integration nur die quadratische Näherung von
berücksichtigt, obwohl zur näherungsweisen Bestimmung der Nullstellen diese bis zur dritten Potenz als
entwickelt wurde. Zum einen erhält man durch die quadratische Reduktion bei der Integration einfache explizite Ausdrücke, zum anderen zeigt eine numerische Analyse, daß der kubische Term gegenüber dem Fehler, welcher durch die ursprüngliche Entwicklung um
entsteht, zunächst vernachlässigt werden kann. Letzterer bedingt einen merklichen Phasenfehler bei größeren Zeiten, kann jedoch durch eine Entwicklung in höheren Potenzen unter Berücksichtigung von
reduziert werden. Dazu verwendet man die Identität
und entwickelt den hinteren Term in eine Potenzreihe. Speziell für
erhält man dann
Der hintere Term korrigiert den Amplitudenfehler, den der vordere Term verursacht. Die nicht aufgeführten Zwischenterme bewirken nur geringfügige Verbesserungen. Mit der Substitution
wird wieder über
integriert. Da
sehr schnell in der Umgebung von
abfällt, kann man
näherungsweise durch
ersetzen, so daß man einen konstanten Korrekturfaktor erhält. Durch diesen erreicht man gegenüber (\ref{eq:Brillouin_Vorlaeufer_2}↓) eine Verbesserung im Phasenverhalten.
Jedoch läßt sich dieses Verfahren nicht für beliebig große Zeiten anwenden. Auch weicht die Sattelpunktnäherung dann immer mehr von der tatsächlichen Lage in der Phasenebene ab. Insbesondere streben die zuvor betrachteten, dem Koordinatenursprung nahen, symmetrisch liegenden Sattelpunkte zu den jeweiligen negativ-wertigen Singularitäten des Verzweigungsschnittes, wo das Integral verschwindet. Die Sattelpunktmethode läßt sich jedoch mit den näherungsweise bestimmten Sattelpunkten bis zum Einsetzen des Hauptsignals mit voller Amplitude anwenden und das Integral numerisch auswerten. Zu beachten ist dann, daß der Nenner
mit weiterer Annäherung von
an
nicht mehr konstant gehalten werden kann, und ab einem bestimmten Zeitpunkt, der durch
gegeben ist, schließlich rechtsseitig der Integrationsweg den Pol im Winkel
passiert, so daß ab diesem das Residuum, welches durch
gegeben ist, zur Funktion (\ref{eq:Signaldarstellung_Brillouin}↓) beiträgt. Der Zeitpunkt liegt bei
mit
und ist daher von der Schwingungsdauer
der anregenden Welle bzw. von
abhängig, so daß man stark unterschiedliche Laufzeiten in Abhängigkeit
erhält. Mit den obigen Parametern ist
. Die zu berechnende Signalfunktion läßt sich mittels der Sprungfunktion
durch
ausdrücken. Der hintere Term
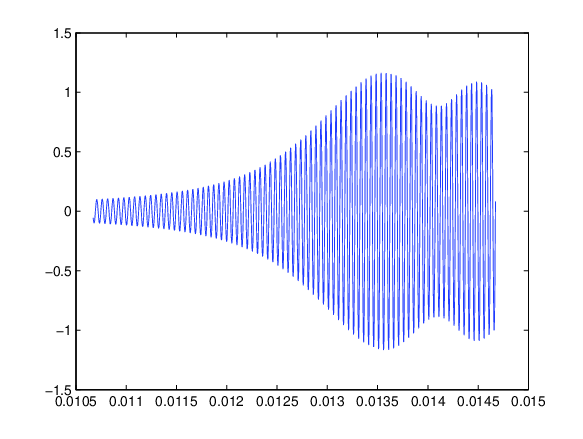
ist der stationäre Wellenanteil, der auch für größere Zeiten verbleibt. Der vordere Integralterm weist mit dem Einsetzen des Residuums einen Phasensprung auf, siehe Abb. 1↓a.
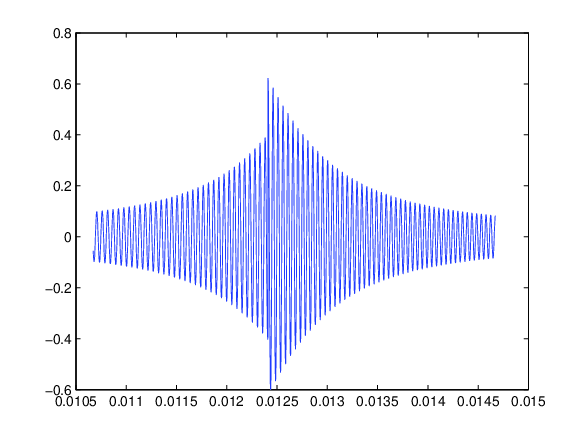
| a) Phasensprungverhalten des Integrals (\ref{eq:Einschwingen}↓) |
|
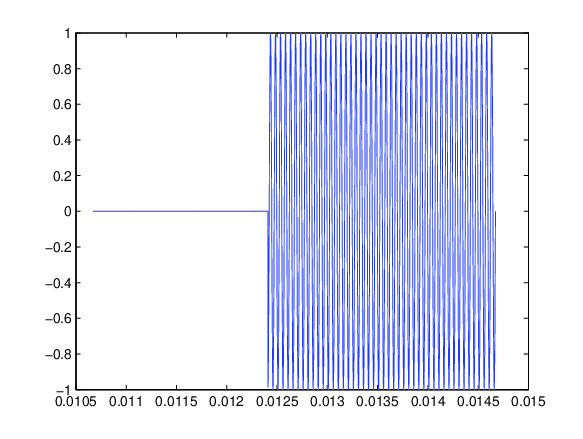
| b) Beitrag des Residuums |
|
Abbildung 1 Signalanteile für (\ref{eq:Einschwingen}↓) in Abhängigkeit von
Für die fernen Sattelpunkte (\ref{eq:Sattelpunkte_fern}↓), bei denen näherungsweise
gilt, kann man ebenfalls eine quadratische Entwicklung
mit
,
und
ansetzen, wofür man gemäß der Formel (\ref{eq: Sattelpunktsnaeherung}↓)
erhält. Für
und
gilt näherungsweise
und damit
bzw. unter Berücksichtigung von
ausgedrückt durch
und
Dies ist entsprechend der Brillouinschen Benennung der erste Vorläufer. Die Näherung ist wegen der Forderung nicht zu kleiner Werte
nur für nicht zu kleine retardierte Zeiten
gültig, also für nicht zu weit entfernte Werte
vom Koordinatenursprung. Der Abschnitt kleiner retardierter Zeiten ist hingegen der Gültigkeitsbereich des Sommerfeldschen Vorläufers. Jedoch ist der Unterschied beider Vorläuferbeschreibungen mit obigen Parametern bis hin zu sehr kleinen
äußerst gering.
Literaturverzeichnis
[1] Sommerfeld, A.: Über die Fortpflanzung des Lichtes in dispergierenden Medien. Annalen der Physik 1914 (10), Band 349, S. 177-202.
[2] Brillouin, L.: Über die Fortpflanzung des Lichtes in dispergierenden Medien. Annalen der Physik 1914 (10), Band 349, S. 203-240.
[3] Debye, P.: Näherungsformeln für die Zylinderfunktionen für große Werte des Arguments und unbeschränkt veränderliche Werte des Index. Math. Ann. 67 (1909), S. 535–558.
[4] Brillouin, L.: Wave propagation and group velocity. Academic Press New York and London, 1960.